RESEARCH ARTICLE
Gompertz’ Hazard Law as a Network Principle of Aging
Jakob Korf 1, *, Arthur A. Sas2
Article Information
Identifiers and Pagination:
Year: 2019Volume: 7
First Page: 14
Last Page: 20
Publisher ID: TOBIOJ-7-14
DOI: 10.2174/1874196701907010014
Article History:
Received Date: 03/12/2018Revision Received Date: 25/03/2019
Acceptance Date: 22/04/2019
Electronic publication date: 31/05/2019
Collection year: 2019

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
Life-spanning population survivorship curves (the number of survivors versus age) are conventionally regarded as a demographic issue. Most often, the term hazard, the relative mortality per age-interval, is used as a typical survivorship parameter. Population survivorship curves are construed from cross-sectional data (single event per individual; here, mortality).
Objective:
We tested (quantitatively) how Gompertz’ law describes the mortality pattern of a wide variety of organisms, some of them fed with lifespan affecting diets. Moreover, we tested (semi-quantitatively) whether Gompertz’ law describes the disintegration of a (biological) small-world network.
Methods:
The Gompertz tests, explored in demographic data of humans (male/female) and 4 animal species (mice, honeybees, fruit flies, houseflies), were analyzed with conventional software. The Gompertz law was examined in a small-world network model.
Results:
Gompertz' law applies to all cohorts; thus, with or without exposure to experimental conditions. It describes in all cohorts old-age slowing of mortality. Gompertz’ law is compatible with a gradual and random increase of connections in the network model.
Conclusion:
Old-age deceleration of mortality is a characteristic of many populations. Aging has to be understood as a lifetime increasing of excitatory or, alternatively, of decreasing inhibitory (biological) connections, thereby facilitating pathogenic mechanisms.
1. INTRODUCTION
Population survivorship curves are used to assess quantitative parameters associated with aging or interventions affecting the longevity of human and animal populations [1-4]. These curves, showing all-cause mortality, do not disclose a specific pathology. Instead, they emphasize general characteristics of aging processes, including a multiplicity of molecular processes [1-4]. Survivorship patterns have been explained by assuming individual (often Gaussian) variability in, among others, frailty, genes or defective proteins [5, 6]. In his classical report, Gompertz [7] suggested that “death may be the consequence of two generally coexisting causes; the one, chance, without a previous disposition to death or deterioration; the other, an unspecified force that destroyed the material of organization necessary for life” [quoted in 1]. The present report describes an approach that might clarify a biological principle underlying population survivorship curves.
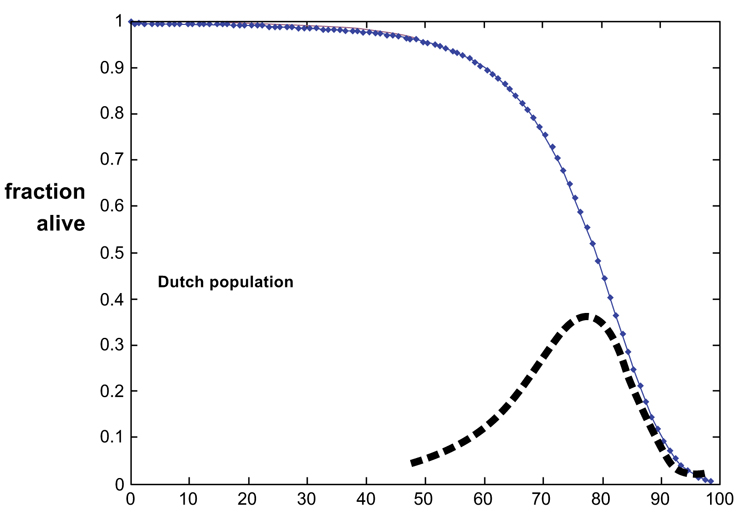
In a protective environment (i.e. with little external causes of death such as severe infections, starvation, and accidents), survivorship curves are population-specific characteristics. Western human and many laboratory animal survival curves show relatively little mortality during the first period of life, but the number of survivors declines approximately exponentially thereafter. The human survivorship curves show long periods (almost 60 years in the Netherlands) of low mortality. At an advanced age, mortality might attenuate [1, 2, 4, 8, 9]. This deceleration has often remained unnoticed or was questioned [8-10]. As discussed below, additional aging-dependent mechanisms might be involved. In a previous report, we argued that the Gompertz approach distinguishes general aging effects and the risk of developing pathologies, such as some forms of cancer and genetic disorders [4]. The present report examines whether the Gompertz approach, including old-age deceleration of survivorship, applies to various animal species, and whether Gompertz’ law is compatible with the increase of small network connectivity.
Our approach is based on the application of the ergodicity principle to population survivorship data. According to (simplified) statistical thermodynamics, ergodicity implies that the distribution of a large number of (identical) particles (or functions) across subcompartments (or space) equates the probability of a single particle to be found in a particular subcompartment. In conventional terminology: in an ideal system, cross-sectional observations (here, spatial dimensions) equate longitudinal observations (here, time courses). Ergodicity of a system is guaranteed if the final state is irreversible, i.e. all constituting elements (i.e. particles) sooner or later end in that final state (here, death) [4, 10, 11]. The principle of ergodicity, i.e. the equivalence of cross-sectional and longitudinal data, can be illustrated with an intuitively easily understandable example of human growth curves: weight versus age. In a population of (young) subjects, these curves can be composed following either of two strategies. First, the longitudinal approach: recruit a representative group of babies, weigh them frequently (e.g. every 4 months) and follow them until adulthood (e.g. 18 years); compose (compute or simulate) the growth curve for every individual and calculate the average (and the deviation) of the essential parameters. The alternative, the cross-sectional approach, is to recruit a large group of youngsters of various ages (babies and children up to 18 years), weigh them, register their age, and calculate the best fitting curve. In the ideal experiment (and in principle), the two computed growth curves are identical and at least one person of the cohort approximates this “ideal” growth curve. Only the second strategy is useful here because the survivorship data and curves are composed with cross-sectional data, as individual measurements can obviously be done only once.
We applied the idea of ergodicity to Gompertz’ law, which is among the best models to describe population survivorship. In contrast to various other models, it describes a wide variety of data sets fairly accurately with two parameters [e.g 1, 2, 4, 7.]. Most population survivorship studies use Gompertz' law to assess the aging-related hazard (the fraction of a population of a defined age interval that dies in that interval), which is modeled as a single exponential age-function. In Kirkwood's words [2], “In essence, the (Gompertz) equation represents a force of mortality that increases exponentially with age in such manner that a hazard parameter grows linearly.” The Gompertz law has been applied to distinguish the increasing force of mortality and the vulnerability to the genetic (dispositional) contribution [11]. In the latter report, only the mortality during the first episode of survival (which is when half of the population dies) was used. Although during that episode, the initial force of mortality can be approximated, it does ignore the capacity of an organism to affect or even counteract mortality. The present report explores Gompertz' law to model the mortality pattern of a population from birth to death and uses the aging-related number of all survivors of a population for the calculations. Accordingly, the hazard function was integrated and subsequently used for modeling. As far as we know, this strategy has only been explored in a human population [4]; here we examine data of a variety of animals, some exposed to lifetime extending interventions. The present approach provides an explanation of the shift from accelerating mortality at younger ages to its deceleration at old age. The calculated ages of inflection of the species tad examined are reported here.
It has been speculated that aging and aging-associated pathology are related either to random damage or to characteristics already present at birth. We searched for a bridging concept. A well-fitting model was found in reports on small-world networks [12]. The idea is as follows: consider a living system or a part of it (organism, organ or cell) as a well-organized cluster of entities and consider that the process of aging gradually affects that organization. Most current network models focus on the opposite direction of temporality: the realization of an organized system starting with randomly active entities (as, for instance, how clocks, “oscillators”, become synchronized through weak interactions [12, 13]). Synchronization depends on the strength of coupling: above a certain threshold, the entities synchronize. Aging might be considered the reverse process: a well-synchronized (or coupled) system gradually disintegrates over time.
We tested whether the Gompertz law explains lifetime mortality patterns, including old-age deceleration of mortality. In this respect, the present report is an extension of our previous study on human data [described in 4] and now includes animal data. We show that the pattern of all-cause mortality clearly deviates from a Gaussian distribution (it is skewed). In addition, we tested the hypothesis of whether a Gompertz pattern of mortality is compatible with the dissolution of a small-world network [12, 13]. This idea was tested semi-quantitatively with an overlay method [4].
2. MATERIALS AND METHODS
2.1. Gompertz’ Function and Applications
The model. Eq 1 shows Gompertz’ expression of the proportional hazard rate µ(t) as a function of age (t); α and β are population specific constants:
| μ (t) = α eα t | (1) |
Reformulation and integration of equation 1 by taking the size of the original population S0 at birth (= 1 after normalization) and S(t) as the relative size of the population at age t gives:
| S (t) = ec(1–ek t) | (2) |
The parameters c and k are population-specific constants. They were used instead of α and β to distinguish them from equation 1. The derivative of Eq 2, m(t), gives the mortality rate at age t:
| m (t) = – k c S (t) ekt | (3) |
Eq (3) is negative because of the decreasing number of survivors during aging.
One implication of Gompertz’ law is that, after an initial increase, the relative mortality decreases at old age. Using the derivative of equation 3, or dm/dt = 0 at tad, we calculated the age of inflection tad, in Eq 4 when an accelerated rate of mortality transits into decelerating mortality:
| ta d = k-1 ln c-1 | (4) |
Notice that tad is independent of the population size.
2.2. Data Sets
We fitted data for a wide variety of cohorts chosen rather arbitrarily from literature or acquired through personal contacts. The following data sets were used: 1) males and females (Dutch population [www.cbs.nl;4 acknowledged]); 2) normally fed mice and during caloric restriction [14, 15]; 3) houseflies (Musca domestica) fed with a variety of diets [16]; 4) West-Indian fruit flies (Anastrepha obliqua) males and females [17,18]; 5) honeybees (Apis melifera) [19]. We estimated tad of the populations shown in the table.
2.3. Quantitative and Semi Quantitative Fits
Gompertz fittings were done using Graph Pad Prism 5 (non-linear regression analysis), resulting in two free parameters, c (no dimension) and k (k in days-1), The confidence intervals and tad were also calculated. As indicated, we examined the mortality pattern of the entire populations (from birth to death), not the hazard function. The network hypothesis was tested with the overlay procedure. We took the network graphs from the figures describing increasing connectivity and hence decreasing lengths of the pathway between the hubs [12]. This approach was applied to illustrate its similarity with the network model of Watts and Strogatz [12, 13]. The overlay procedure [4] allows to optimizing the similarity between the fits of 2-dimensional (XY) graphs by laying the mathematical graph (i.e. Gompertz graph taken from the internet) over the survivorship data. By varying the length of the X and Y axis, the similarity between graphs can be assessed. The similarity was estimated by visual inspection and by computations. Accordingly, the correlation between Gompertz’ fitting and network connectivity was determined by taking approximately 100 time-points (the human curve: corresponding to yearly survivorship).
3. RESULTS AND DISCUSSION
Figs. (1 and 2) show the survivorship data and fitted curves. Table 1 shows the quantitative data. The quantitative fits and parameters illustrate that Gompertz’ equation provides good fits with survival data of the Dutch population and of nearly all animal species. The derivative of the Gompertz curve emphasizes the lifetime asymmetry, thus deviating from a Gaussian distribution. Minor deviations were noticed in the data of ad libidum fed mice, but not in those of the calorie-restricted fed mice. These results support the quantitative analyses, showing both the wide applicability of the fits and the advanced-age deceleration of mortality of all tested populations. In all populations, the tad is later than the 50% mortality age. The present analysis illustrates that the Gompertz law is incompatible with a Gaussian distribution of individual properties over the population, as being time-asymmetrical. Gaussian distribution is either inadequate or a possible time-symmetry disappears during aging. In Fig. (1), tad is not time-symmetrically positioned.
The overlay approach to compare the Gompertz law with a small-world network pattern is shown in Fig. (3). The function assessed is the Gompertz graph decreasing from 100% towards 0% survival. This analysis shows that a change of connectivity increases every 25 years by a factor 10. Correlation between the Gompertz curve and the network curve is more than 0.99. in fact, the overlap is maximal. Thus in practice, the curves are identical (except perhaps at very high age). The network approach discloses increasing connectivity between entities, which ends (perhaps counter-intuitively) as an infinitely randomly active state. A possible interpretation of the network analysis is given below.
4. BIOLOGICAL IMPLICATIONS
Old-age mortality deceleration has often remained unnoticed or has even been rejected by some demographic investigators. For instance, Gavrilova and Gavrilov [20, and their previous reports] were unable to observe a decline of the mortality rate in humans of advanced age and rodents. The difference in their conventional approach is that their hazard functions are based on the mortality of subcohorts of the entire population taken over a fixed period of approximately one year. Gavrilova and Gavrilov [20] correctly noticed “that the famous Gompertz law was suggested to fit hazard rate (mortality force), rather than the probability of death.” But they erroneously suggested [20], that the deceleration of mortality implies “near non-aging” at an advanced age [also discussed in 1, 2, 4, 10]. In contrast: the present analysis does indeed point to a continuously increasing hazard function, but it implies that the evolving pattern of mortality depends on additional aspects of an organism, possibly related to their complexity. Hughes and Hekimini [11] in principle use the here defined equation 1 and the 50% survivorship as a measure for aging. Fig. (1) of our present study illustrates that this function is not time-symmetric and differs from a Gaussian distribution of survivorship. Our approach emphasizes that aging is a time–associated process, rather than a distribution of entities with more or less equivalent properties. Nevertheless, we acknowledge that the distribution curve shown in Fig. (1) approximates a Gaussian distribution and such approximation might incidentally be useful, as shown by Hughes and Hekimi [11].
In a previous study, we examined the incidence of cancer using a semiquantitative method [4]. The incidence of a variety of cancers (new diagnoses per year per 100,000 persons) shows an almost exponential increase during aging [21-24], but at higher ages, the incidence rate is less than predicted by the exponential function [21]. The incidence of prostate and colon cancer was nearly identical with the survivorship curves for the entire population, including a tendency of old-age deceleration, whereas the incidence data on cervix carcinoma clearly deviate from Gompertz’ law. Indeed, the latter cancer is caused by an infection of the papillomavirus at a young age. Our approach distinguishes predominantly intrinsically aging-associated versus extrinsically caused mortality. Moreover, the mortality and morbidity during aging might be the combined consequence of general aging and specific pathologies. Attempts to identify specific pathogenic mechanisms or the involvement of particular genes should take both principles into account. The process of general aging might stimulate the expression of some pathogenic mechanisms in an age-dependent way. Old-age deceleration of mortality might serve as an example of such a possibility. pathology [4]. The Gompertz function might then describe the combined consequences of both the risk of increasing damage during lifetime (hazard) and the capacity of the organism to compensate or combat the expression of (at least some) pathological processes.
| Population |
Parameter c (95% CI) |
Parameter k (days -1) (95% CI) |
Absolute Sum of Squares | tad |
|---|---|---|---|---|
|
Dutch Population 2003 Male + Female (n ≈15,000,000) |
1.74 * 10-4 (1.54 * 10-4 – 1.94 * 10-4) |
2.87* 10-4 (2.74*10-4 – 2.85*10 -4) |
0.007149 | 86.5 years |
|
Dutch Population 1994 Male (n ≈ 7,585,000) |
3.52 * 10-4 (3.20 * 10-4 – 3.85 * 10-4) |
2.76 10 -4 (2.66*10-4 – 2.73* 10-4) |
0.005600 | 80.0 years |
| Female (n ≈ 7,755,000) |
1.12 * 10-4 (9.41 * 10-5 – 1.30 * 10-4) |
2.95*10 -4 (2.82*10-1 – 2.93* 10-4) |
0.01212 | 86.6 years |
|
Mouse Fed Normally (n = 60) |
1.28 * 10-3 (5.14 * 10-4 – 2.04 * 10-3) |
6.87* 10 -3 (6.23*10-3 –7.50*10-3) |
0.07075 | 32.3 months |
| Caloric Restriction (n = 60) |
9.63 * 10-4 (5.88 * 10-4 – 1.33 * 10-3) |
6.13 *10-3 (5.80* 10-3 – 6.50*10-3) |
0.03123 | 37.7 months |
|
House Fly Diet I (n = 200) |
3.28 * 10-2 (2.70 * 10-2 – 3.89 * 10-2) |
1.58 *10-1 (1.49*10-1 –.66 * 10-1) |
0.02111 | 21.6 days |
| Diet V (n = 200) |
1.80 * 10-2 (1.45 * 10-2 – 2.16 * 10-2) |
1.36 * 10-1 (1.29*10-1 –1.43*10-1) |
0.02785 | 29.5 days |
| Diet VI (n = 200) |
3.26 * 10-3 (2.72 * 10-3 – 3.80 * 10-3) |
1.61 * 10-1 (1.56 *10-1–1.66*10-1) |
0.01091 | 35.6 days |
|
Fruit Fly Male (n = 162,280) |
6.44 * 10-1 (5.62 * 10-1 – 7.25 * 10-1) |
5.26 * 10-2 4.85*10-2-5.68*10-2) |
0.02145 | 44.1 days |
| Female (n = 134,807) |
8.85 * 10-1 (8.26 * 10-1 – 9.45 * 10-1) |
3.63 * 10-2 (3.47*10-2–3.80*10-2) |
0.00630 | 31.1 days |
|
Honey Bee Male (n = 200) |
3.96 * 10-2 (3.11*10-2 – 4.82*10-2) |
9.42 * 10-2 (8.81*10-2 –1.00 * 10-1) |
0.05360 | 34.3 days |
 |
Fig. (2). Examples of quantitative Gompertz fits of survivorship curves. A: Dutch male population, B: Dutch female population: C: House flies on various diets: Diet 1; left curve; Diet V; middle curve and Diet VI; right curve. D: Honeybees (males) under normal conditions; E: B6-mice fed ad libidum; F: B6-mice calory restricted diet. Black dots are observational data (yearly survival data of the human population; weekly or daily survival in the animal studies); lines are the best fitting curves. All examples show a deceleration of mortality at an advanced age. Quantitative data in Table. 1 |
Gompertz' mortality function is bi-exponential, suggesting the existence of at least two active biological principles [4]. First, the exponential function, characterized by a continuously mono-exponential decline and not taking into account some sort of linear aging dependence. The latter has to be incorporated in case of aging-independent risk of mortality, which is negligible in the Dutch data. Hence, the so-called Makeham correction, to account for accidents or fatal inborn errors, can be ignored. At time zero (t=0), the exponential function is zero, whereas, at old age, this function becomes highly negative. But, considering the complete Gompertz function, the impact of high values of the exponent “causes” a slowing down of mortality at an advanced age. If the initial mono-exponential function has some direct relationship with accumulating damage, then the complete function suggests that the impact of such damage is continuously attenuated. It is as if the expression of damage and/or the consequences of damage for mortality become gradually impaired during aging. Previously, we have suggested that the expression of fatal damage (e.g. cancer or arteriosclerosis) requires a vital organism to express
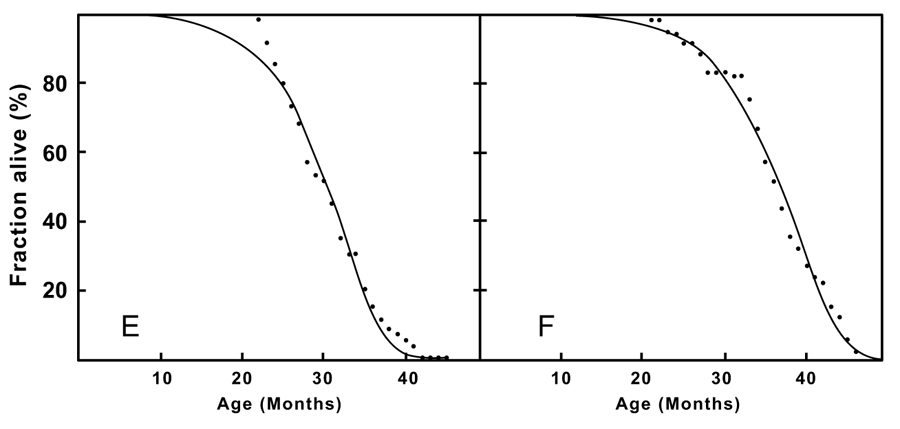 |
Fig. (3). Example of the similarity network model and Gompertz' law. Overlay procedure (described in 4). The semi-quantitative approach shows that an increasing number of connections (clustering) eventually leads to some random structure. In the original model of the authors, clustering indicates the increasing number of connections between entities. The present concept of clustering (aging, leading to a decrease of survivors [12, 13];) is considered a parameter of increasing loss of connections between interacting entities (clustering) so that the organization of a living system gradually becomes lost. Accordingly, we suggest that aging is an apparently increasing loss of inhibitory or regulatory connections. The emerging result is an uncontrolled and possibly pathogenic activity of the thus affected structure. |
CONCLUSION
The hypothesis defended here that Gompertz' hazard population law discloses an aging principle of every individual of that population was thus far tested only indirectly. Gompertz’ law accurately describes lifetime patterns of acceleration and deceleration of mortality of a wide variety of organisms, including humans. This conclusion applies to untreated organisms, to lifespan-extending interventions and also to the incidence of aging-associated pathologies [4]. We propose that the consequences of aging on the functioning of an organism might be understood in a network model. We suggest that the loss of connectivity in a network is concomitant with less control of the constituting entities. These disconnections might ultimately increase the risk of developing fatal pathogenic processes. In other words, the proposed increasing randomness of connectivity might point towards an increasing number of freedom parameters of the disconnected entities. The proposed network model does not necessarily apply to the whole organism, but may also apply to cell aggregates or organs that are critically involved in vital functions of the organism.
Our conceptualizations of Gompertz' law and network models imply that deterioration of functions is a continuous process starting at birth, and not after reproductive success (as suggested in [1]). The apparent rate of disintegration of human female and male survivorship curves are almost similar, which is not well compatible with the notion that the female reproductive period (being determined by the exponential loss of fertilizable ova) ends earlier than the male reproductive capacity, which remains largely intact at older age. Age-related diseases have to be viewed from two perspectives: many of them (e.g. cancer, cardiovascular diseases) closely follow Gompertz' aging law, suggesting that the expression of pathology not only depends on a particular pathogenic process but to a substantial extent also on the actual state (or network connections) of the organism or its organs [4]. One challenge could be how to identify the biological basis of the network connections and to understand their role in senescence.
We acknowledge that the present network analyses are based on semiquantitative analyses. Nevertheless, our interpretation of Gompertz' law might help to develop biologically relevant aging laws, as was attempted here using network models. Accordingly, Gompertz' law might be understood as a gradual dissolution of networks. Direct testing of our proposal requires dedicated studies of age-related functions of individual organisms, their cells or organs. Our approach might also be seen as an invitation to develop quantitative (mathematical) models to prove the compatibility of Gompertz’ law with network models.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of the article is available in the Bureau of statistics (CBS, The Netherlands) at www.cbs.nl and in the Integraal Kanker Centrum Nederland (IKN Integral Dutch Cancer Center) at www.iknl.nl
FUNDING
The study was supported by the University Medical Center Groningen and the University of Groningen.
CONFLICT OF INTEREST
The authors declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The discussions with and contributions of Albert Mollema, Bennard Doornbos, Hans Burgerhof, Harold Snieder, and Doekele Stavenga are highly appreciated. Myrthe Korf edited the final version.
REFERENCES
| [1] | Carnes BA, Olshansky SJ, Grahn D. Continuing the search for a law of mortality. Popul Dev Rev 1996; 22: 231-64. |
| [2] | Kirkwood TBL. Deciphering death: A commentary on Gompertz (1825) ‘On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies’. Philos Trans R Soc Lond B Biol Sci 2015; 370(1666): 370-9. |
| [3] | Partridge L. The new biology of ageing. Philos Trans R Soc Lond B Biol Sci 2010; 365(1537): 147-54. |
| [4] | Sas AA, Snieder H, Korf J. Gompertz’ survivorship law as an intrinsic principle of aging. Med Hypotheses 2012; 78(5): 659-63. |
| [5] | Strehler BL, Mildvan AS. General theory of mortality and aging. Science 1960; 132(3418): 14-21. |
| [6] | Kirkwood TBL. Understanding the odd science of aging. Cell 2005; 120(4): 437-47. |
| [7] | Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Phil Trans Roy Soc London A B 1825; 11: 513-85. |
| [8] | Vaupel JW, Carey JR, Christensen K, et al. Biodemographic trajectories of longevity. Science 1998; 280(5365): 855-60. |
| [9] | Vaupel JW, Baudisch A, Dölling M, Roach DA, Gampe J. The case for negative senescence. Theor Popul Biol 2004; 65(4): 339-51. |
| [10] | Fisher AJ, Medagli JD, Jeronimus BF. Lack of group-to-individual generalizability is a threat to human subjects research. Proc Natl Acad Sci 2018; 115: E 6106-6115. |
| [11] | Hughes BG, Hekimi S. Different mechanisms of longevity in long-lived mouse and Caenorhabditis elegans mutants revealed by statistical analysis of mortality rates. Genetics 2016; 204(3): 905-20. |
| [12] | Strogatz SH. From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Physica D 2000; 143(1-4): 1-20. |
| [13] | Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature 1998; 393(6684): 440-2. |
| [14] | Dhahbi JM, Kim HJ, Mote PL, Beaver RJ, Spindler SR. Temporal linkage between the phenotypic and genomic responses to caloric restriction. Proc Natl Acad Sci USA 2004; 101(15): 5524-9. |
| [15] | Harrison DE, Strong R, Sharp ZD, et al. Rapamycin fed late in life extends lifespan in genetically heterogeneous mice. Nature 2009; 460(7253): 392-5. |
| [16] | Cooper TM, Mockett RJ, Sohal BH, Sohal RS, Orr WC. Effect of caloric restriction on life span of the housefly, Musca domestica. FASEB J 2004; 18(13): 1591-3. |
| [17] | Edman U, Garcia AM, Busuttil RA, et al. Lifespan extension by dietary restriction is not linked to protection against somatic DNA damage in Drosophila melanogaster. Aging Cell 2009; 8(3): 331-8. |
| [18] | Garcia AM, Calder RB, Dollé MET, Lundell M, Kapahi P, Vijg J. Age- and temperature-dependent somatic mutation accumulation in Drosophila melanogaster. PLoS Genet 2010; 6(5)e1000950 |
| [19] | Oliver R. Understanding Colony Build up and Decline Part 5. Egg laying, adult survivorship, and modelling colony growth 2015. Available at: http://scientificbeekeeping.com/understanding-colony- buildup-and-decline-part-5/ |
| [20] | Gavrilova NS, Gavrilov LA. Biodemography of old-age mortality in humans and rodents. J Gerontol A Biol Sci Med Sci 2015; 70(1): 1-9. |
| [21] | Little MP. Cancer models, genomic instability and somatic cellular Darwinian evolution. Biol Direct 2010; 5: 19. |
| [22] | Hornsby C, Page KM, Tomlinson IP. What can we learn from the population incidence of cancer? Armitage and Doll revisited. Lancet Oncol 2007; 8(11): 1030-8. |
| [23] | Hornsby C, Page KM, Tomlinson I. The in vivo rate of somatic adenomatous polyposis coli mutation. Am J Pathol 2008; 172(4): 1062-8. |
| [24] | Reed MJ, Karres N, Eyman D, Cruz A, Brekken RA, Plymate S. The effects of aging on tumor growth and angiogenesis are tumor-cell dependent. Int J Cancer 2007; 120(4): 753-60. |